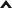Структура ИПМИ
Лаборатория информационных компьютерных технологий
руководитель: к.т.н. Крижановский Андрей Анатольевич
Основные направления научных исследований
Научно-исследовательская работа
Основные результаты деятельности
Публикации
Сотрудники
Контактная информация
Основные направления научных исследований
Основные результаты деятельности
Сотрудники лаборатории информационных компьютерных технологий добились результатов в следующих научных областях:Сетевые игры оптимальной маршрутизации
В игре максимизации минимальной задержки системы обслуживания для общего случая N машин найдена нижняя граница цены анархии и для случая трех машин найдено ее точное значение. Для двух машин доказано, что при добавлении в систему новой третьей машины цена анархии не изменяется, либо растет. Предложен алгоритм вычисления точного значения цены анархии на примере системы трех машин [1].
Цена анархии для системы S четырех машин с малыми значениями скоростей
Корпусная лингвистика и обработка текста на естественном языке
 В 2009—2016 году сотрудниками ИЯЛИ и ИПМИ под руководством Зайцевой Н.Г. был создан онлайн «Корпус вепсского языка». Словарь корпуса содержит около 10 тысяч лемм и словоформ, включает переводной словарь с вепсского на русский и английский языки. Тексты корпуса разделены на подкорпуса: диалектные тексты, вепсские причитания, вепсские народные сказки, библейские тексты, младописьменный подкорпус (художественные и публицистические тексты). Первые три подкорпуса являются параллельными и включают переводы на русский язык. Текстов в корпусе насчитывается более тысячи [2].
В 2009—2016 году сотрудниками ИЯЛИ и ИПМИ под руководством Зайцевой Н.Г. был создан онлайн «Корпус вепсского языка». Словарь корпуса содержит около 10 тысяч лемм и словоформ, включает переводной словарь с вепсского на русский и английский языки. Тексты корпуса разделены на подкорпуса: диалектные тексты, вепсские причитания, вепсские народные сказки, библейские тексты, младописьменный подкорпус (художественные и публицистические тексты). Первые три подкорпуса являются параллельными и включают переводы на русский язык. Текстов в корпусе насчитывается более тысячи [2].Ряд текстов, включённых в корпус, собирался на протяжении десятилетий сотрудниками ИЯЛИ в ходе полевых исследований. При лингвистическом анализе текста нужна информация о том, где и когда был записан текст, поэтому в корпусе большое внимание уделено метаинформации и описанию текстов. В паспорте текста указана библиографическая информация о месте и дате записи, имени и месте рождения информанта, имени сотрудника, записавшего текст и так далее. Корпус включает более 800 библиографических источников [2].
Авторы проекта «Корпус вепсского языка» (ИПМИ и Институт языка, литературы и истории КарНЦ РАН) в 2017 году получили премию "Ключевое слово" в номинации "За лучший научный проект". Премия учреждена Федеральным агентством по делам национальностей (ФАДН России).
В 2016 году на основе "Корпуса вепсского языка" был создан "Открытый корпус вепсского и карельского языков" (ВепКар). Это многоязычный корпус, включающий тексты на вепсском и карельском языках, некоторые тексты содержат перевод на русский язык [3]. Особенностью базы данных и самого корпуса ВепКар является тесная взаимосвязь словарей и текстов. Многофункциональные словари вепсского и карельского языков содержат толкование, перевод, диалектные пометы, семантические отношения (синонимы, антонимы и др.), примеры словоупотреблений со ссылкой на тексты, а также полные словоизменительные парадигмы. Все тексты автоматически размечаются и от слов в тексте идут отсылки на соответствующие значения в словарных статьях [3]. Исходный код корпусного менеджера Dictorpus, обеспечивающего доступ к данным ВепКар, доступен на условиях открытой мультилицензии. Тексты и словари корпуса ВепКар распространяются по открытой лицензии CC BY. Информация о корпусе доступна на YouTube (плейлист VepKar) и в Википедии (Category:VepKar).
Разработаны алгоритмы определения части речи и грамсета по данным морфологического словаря карельского языка. Словарь содержит 3000 лемм, из них 2500 лемм привязаны к 128 тысячам словоформ. Для каждой словоформы известны лемма, часть речи и набор грамматических признаков (грамсетов). Были сформулированы и запрограммированы правила генерации словоформ по части речи, грамсету и набору псевдооснов [9].
В течение 2019-2021 годов были сформулированы и запрограммированы правила именного и глагольного словоизменения для всех диалектов вепсского языка и его младописьменного варианта, а также для ливвиковского, севернокарельского и тверского новописьменных вариантов карельского языка. Благодаря этому в системе ВепКар в полуавтоматическом режиме было сгенерировано более 2 млн словоформ [10].
В 2019 году данные корпуса VepKar были экспортированы в формате CONLL для использования в соревновании морфологических анализаторов для малоресурсных языков [11].
Разработаны алгоритмы определения части речи и грамсета по данным морфологического словаря карельского языка. Словарь содержит 3000 лемм, из них 2500 лемм привязаны к 128 тысячам словоформ. Для каждой словоформы известны лемма, часть речи и набор грамматических признаков (грамсет). Были сформулированы и запрограммированы правила генерации словоформ по части речи, грамсету и набору псевдооснов [12].
Литература
- Чиркова Ю.В. Цена анархии в задаче максимизации минимальной задержки машин в системе обслуживания // Управление большими системами, вып. 62. 2016. C. 30-59.
- Зайцева Н. Г., Филатова М. М., Шибанова Н. Л., Крижановский А. А. Корпус вепсского языка // Труды международной конференции «Корпусная лингвистика ‒ 2015». — СПб.: СПбГУ, 2015. — С. 202-212. — ISBN 978-5-8465-1498-0.
- Т.П. Бойко, Н.Г. Зайцева, Н.Б. Крижановская, А.А. Крижановский, И.П. Новак, Н.А. Пеллинен, А.П. Родионова, Е.Д. Трубина. Лингвистический корпус ВепКар – «заповедник» прибалтийско-финских языков Карелии // Труды КарНЦ РАН. No 7. Комплексные научные исследования КарНЦ РАН. 2021. C. 100-115 DOI: 10.17076/them1415
- Кириллов А.Н. Динамические системы с переменной структурой и размерностью // Известия вузов. Приборостроение. 2009. Т.52, №3. С.23–28.
- Кириллов А.Н. Моделирование динамики структур гибридных систем. –Информационно-управляющие системы. 2011, № 4, с. 42-46.
- Кириллов А.Н. Метод динамической декомпозиции в моделировании систем со структурными изменениями. - Информационно – управляющие системы. 2009. №1. – С.20 - 24.
- Kirillov A., Starkov V. Some extensions of the Poincaré–Birkhoff theorem // Journal of Fixed Point Theory and Applications. Vol. 13. № 2. 2013. P. 611–625
- Alexander Kirillov and Victor Starkov. Fixed points of infinitely connected domain continuous mappings // Fixed Point Theory. V. 16. No. 1. 2015. P. 103–106
- Krizhanovsky A., Krizhanovskaya N., Novak I. Part of speech and gramset tagging algorithms for unknown words based on morphological dictionaries of the Veps and Karelian languages // Management in Data Intensive Domains. DAMDID/RCDL 2020. Communications in Computer and Information Science, vol 1427. Springer, Cham, 2021. Pp. 163-177 DOI: 10.1007/978-3-030-81200-3_12.
- Новак И.П., Крижановская Н.Б., Бойко Т.П., Пеллинен Н.А. Разработка правил генерации именных словоформ для новописьменных вариантов карельского языка // Вестник угроведения. Т. 10. No 4. 2020. C. 679–691. DOI: 10.30624/2220-4156-2020-10-4-679-691
- Klyachko E.L., Sorokin A.A., Krizhanovskaya N.B., Krizhanovsky A.A., Ryazanskaya G.M. LowResourceEval-2019: a shared task on morphological analysis for low-resource languages // Computational Linguistics and Intellectual Technologies: papers from the Annual conference “Dialogue” (Moscow, May 29— June 1, 2019) Issue 18 (25). 2019.
- Krizhanovsky A., Krizhanovskaya N., Novak I. Part of speech and gramset tagging algorithms for unknown words based on morphological dictionaries of the Veps and Karelian languages // Management in Data Intensive Domains. DAMDID/RCDL 2020. Communications in Computer and Information Science, vol 1427. Springer, Cham, 2021. Pp. 163-177. DOI: 10.1007/978-3-030-81200-3_12
Сотрудники
научный сотрудник, к.ф.-м.н.
ведущий научный сотрудник, д.ф.-м.н., доц.
ведущий инженер-исследователь, ведущий инженер-исследователь МНОЦ NORDICA
младший научный сотрудник, к.ф.-м.н.
ведущий научный сотрудник, д.ф.-м.н., проф.
старший инженер-программист, ведущий инженер-программист отдела ИТС, аспирант ИЛ, младший научный сотрудник лаб. динамики и продуктивности таежных лесов
ведущий научный сотрудник, заместитель директора по научной работе ИПМИ, д.ф.-м.н.
Контактная информация
Официальное название: Институт прикладных математических исследований — обособленное подразделение Федерального государственного бюджетного учреждения науки Федерального исследовательского центра "Карельский научный центр Российской академии наук"Адрес: 185910, Россия,
Республика Карелия,
г. Петрозаводск,
ул. Пушкинская, 11
ИПМИ КарНЦ РАН
Контактный телефон(ы): +7 (8142) 76-63-12
Факс: +7 (8142) 76-33-70
Электронная почта: andrew.krizhanovsky/puppy/gmail.com