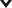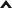В журнале Dynamic Games and Applications опубликована совместная статья директора Института прикладных математических исследований КарНЦ РАН Владимира Мазалова и его коллег из Университета Циндао (Китай). Российский ученый – авторитетный специалист в области теории игр – это раздел математики, посвященный поиску решений конфликтов между участниками той или иной системы и оптимальной стратегии их действий.

Предметом теории игр являются и переговоры, которые всегда предполагают участие двух или более сторон. Теоретико-игровой анализ переговоров широко применяется в политических и экономических науках, в том числе в моделях голосования, использования природных ресурсов, уменьшения загрязняющих выбросов и многих других.

Многие важные консультации или переговоры ведутся сегодня в соцсетях между людьми, связанными, в свою очередь, семейными, дружескими или профессиональными отношениями. Часто принятие решений основывается на консенсусе, достигнутом в ходе таких сетевых переговоров. На окончательное решение могут влиять и внешние факторы: СМИ, политические силы, институты и т.п. Участников социальной сети исследователи в статье называют агентами, а внешние силы, влияющие на их мнение, — игроками. В качестве игроков могут выступать маркетологи или политики. Их цель – максимально приблизить конечное мнение всех пользователей-агентов к желаемому с минимальными затратами на контроль.
По словам авторов, оптимальное управление в этом случае зависит от структуры сетевых коммуникаций. Этот фактор имеет решающее значение: наличие или отсутствие общения между членами сообщества напрямую влияет на постоянный процесс формирования мнений. Однако в большинстве исследовательских работ ранее эта структура игнорировалась. В новой статье ученые рассматривают модель влияния внешнего управления на динамику мнений и конечный консенсус пользователей соцсети.

– Например, есть конкурирующие политические или экономические силы. Для решения какого-то вопроса им необходимо склонить общественное мнение на свою сторону. На это они готовы выделять деньги. В соцсетях важно, на кого влиять. Математика подтверждает: это должны быть люди, имеющие много связей в структуре сети или это может быть человек менее популярный, но который находится в центре событий. Через этих людей проходит вся информация. Надо уметь вычислять их, но в большой сети это бывает трудно сделать. Для этого специалисты строят графы, анализируют их и дают прогноз, – рассказал доктор физико-математических наук Владимир Мазалов.

В этой сфере математическая наука граничит с социальными, в частности, психологией. Например, дифференциальные уравнения учитывают склонность пользователей к подтверждению своей точки зрения — тенденции, когда люди отдают предпочтение информации, которая согласуется с их убеждением или гипотезой. Это также находит отражение в коммуникациях в соцсетях.

В ходе исследования математики изучили варианты, когда на мнение пользователей влияет один или несколько игроков. В первом случае проблема сводится к задаче оптимального управления. С помощью метода динамического программирования ученые представили задачу как систему уравнений, решение которых зависит только от текущего среднего мнения всех агентов в сети и параметров модели и структуры связей.

– Если игрок один, то он сможет привести общее мнение к желаемому консенсусу. Время, за которое это произойдет, зависит от структуры сети. Если сеть разреженная, то ему придется долго добиваться результата, а если связей в ней много, то эффект будет быстрее и дешевле. Затраты в том или ином случае также можно посчитать математически, – отметил директор ИПМИ КарНЦ РАН.

В случае с несколькими игроками, зачастую конкурирующими, пытающимися влиять на общественное мнение, задача представляет собой динамичную игру. Ученые выполнили компьютерное моделирование социальной сети из четырех агентов и рассмотрели различные сценарии с разными взаимоотношениями участников. В результате они пришли к выводам о важности структуры связей в сети и возможностях игроков создавать или удалять связи между агентами для сокращения расходов.

– Если игроков два или больше, то ситуация уже не такая, как в первом случае. Теоремой доказано, что агенты все-таки приходят к консенсусу, но он не будет совпадать с целями игроков – скорее, расположится где-то между ними. Результат также зависит от структуры сети и затрат на контроль, – пояснил Владимир Мазалов.

Исследователи отмечают: в случае нескольких игроков к консенсусу приходят только пользователи, не находящиеся под их влиянием. У агентов под влиянием, например, ангажированных, мнение останется отличным от общего. Скорость достижения консенсуса сильно зависит от того, насколько велика разница между исходным мнением пользователя и тем, которого от него ждут, а также способности игрока влиять на максимальное количество агентов.

Таким образом исследование математиков подтвердило: в современном мире социальные сети – это не только удобное средство коммуникации, но и инструмент влияния на общественное мнение, эффективность которого зависит от количества пользователей и связей между ними.

Фото: Игорь Георгиевский / КарНЦ РАН